Covariance and Correlation

Joint Random variables

More often, in real life, we see two or more random variables related to each other. For example, height of a person is related to weight of a person. Amount of investment is related to amount of return. Or maybe two variables are not related at all, but can occur jointly - flipping a coin and rolling a die.

For simplicity, let's take two random variables A and B.

A = flipping a coin, B = rolling a die

$P(A \cap B) = {1 \over 12} \rightarrow Joint\,random\,variable$

In statistics, we measure how strongly two random variables are related by two metrics - Covariance and Correlation.

Correlation

Positive correlation

A positive correlation exists between two variables A and B when A increases, B also increases and B decreases when A decreases. Graph between A and B would look like the following.

Examples

• Height v/s Weight of a person
• Walking distance v/s calories burnt
• Product quality v/s sales

Perfect Positive correlation

A perfect positive correlation exists if there is a positive linear association between two variables. Which means, given variable A, we can exactly predict the value of B by multiplying with a positive number.

Examples

• Length of a square v/s it's circumference
• Weight in kilos v/s weight in pounds

Negative correlation

A negative correlation exists between two variables A and B, if A decreases when B increases and A increases when B decreases.

Examples

• Mobile screen time v/s remaining battery percentage
• Current run rate v/s Required run rate (in Cricket)

Perfect Negative correlation

A perfect negative correlation exists if there is a negative linear association between two variables.

Examples

• Power v/s focal length of a lens
• Frequency v/s wavelength of light

Zero correlation

If two variables are independent of each other, then there is no correlation or zero correlation.

Examples

• Bitcoin price v/s speed of light
• Your mobile usage per day v/s neighbor's electricity bill

Calculating covariance and correlation

$Covariance(x, y) = { {\sum_{i=1}^n (x_i - \bar{x}) \cdot (y_i - \bar{y})} \over n-1} = E[XY] - \mu_x\mu_y$

$Correlation(x, y) = {Covariance(x, y) \over \sigma_x \cdot \sigma_y}$

import numpy as np
import matplotlib.pyplot as plt

x = np.array([50, 30, 67, 103, 49, 156, 33, 78])
y = np.array([601, 304, 801, 905, 359, 1100, 205, 801])

plt.scatter(x, y)

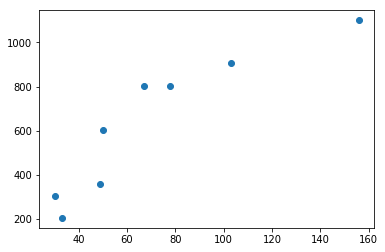
def covariance(x, y):
    if len(x) != len(y) or len(x) < 1: return None
    mean_x, mean_y = np.mean(x), np.mean(y)
    numerator = np.sum([(a - mean_x) * (b - mean_y) for (a, b) in zip(x, y)])
    return numerator / (len(x) - 1)

def correlation(x, y):
    cov = covariance(x, y)
    if cov: return cov / (np.std(x, ddof=1) * np.std(y, ddof=1))

print(f'Covariance = {covariance(x, y)}')
print(f'Correlation = {correlation(x, y)}')

Covariance = 12194.142857142857
Correlation = 0.9072220542468226

Variance of sum and difference

If we have two random variables X and Y,

Variance of X + Y is given by,

$Var(X + Y) = \sigma_x + \sigma_y = \sigma_x^2 + \sigma_y^2 + 2 \cdot Cov(X, Y)$

Variance of X - Y is given by,

$Var(X - Y) = \sigma_x - \sigma_y = \sigma_x^2 + \sigma_y^2 - 2 \cdot Cov(X, Y)$